A Very Quick Guide To Calculating Big O Computational Complexity
Big O: big picture, broad strokes, not details
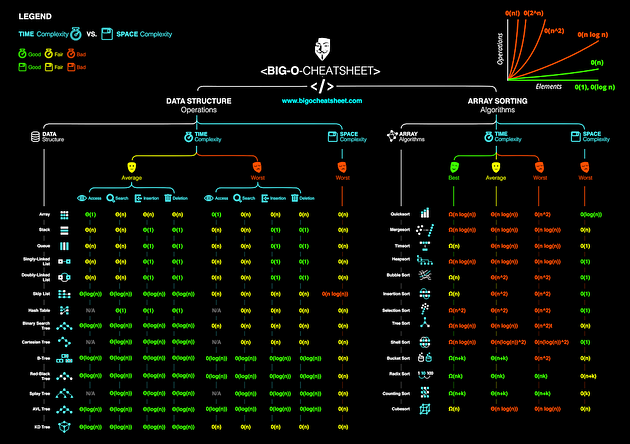
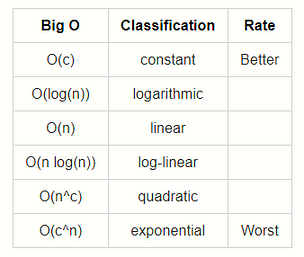
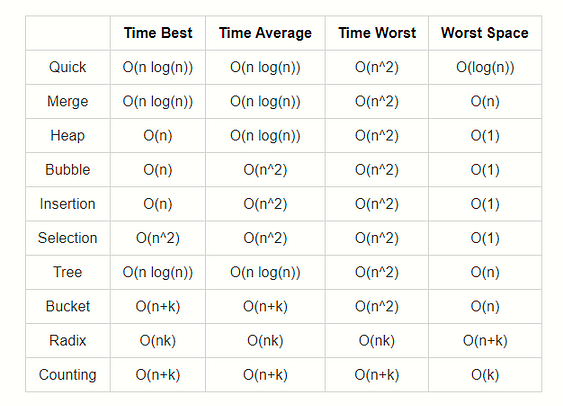
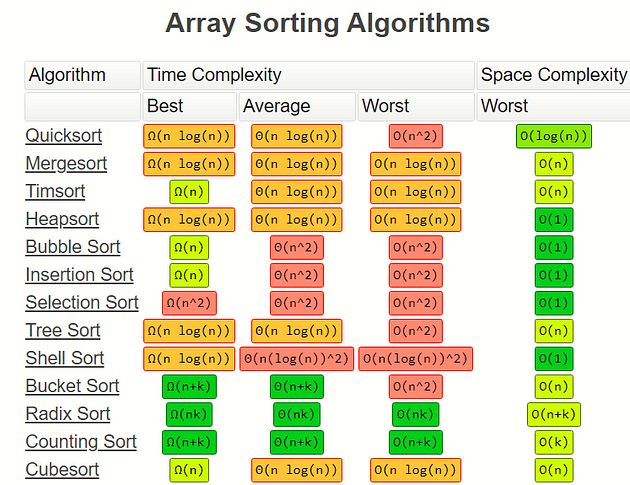
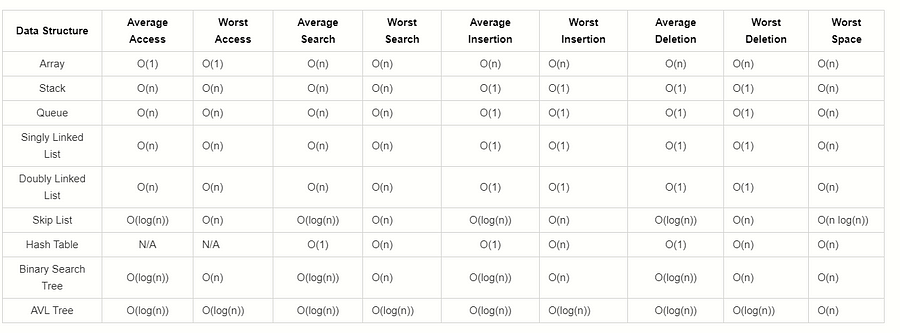
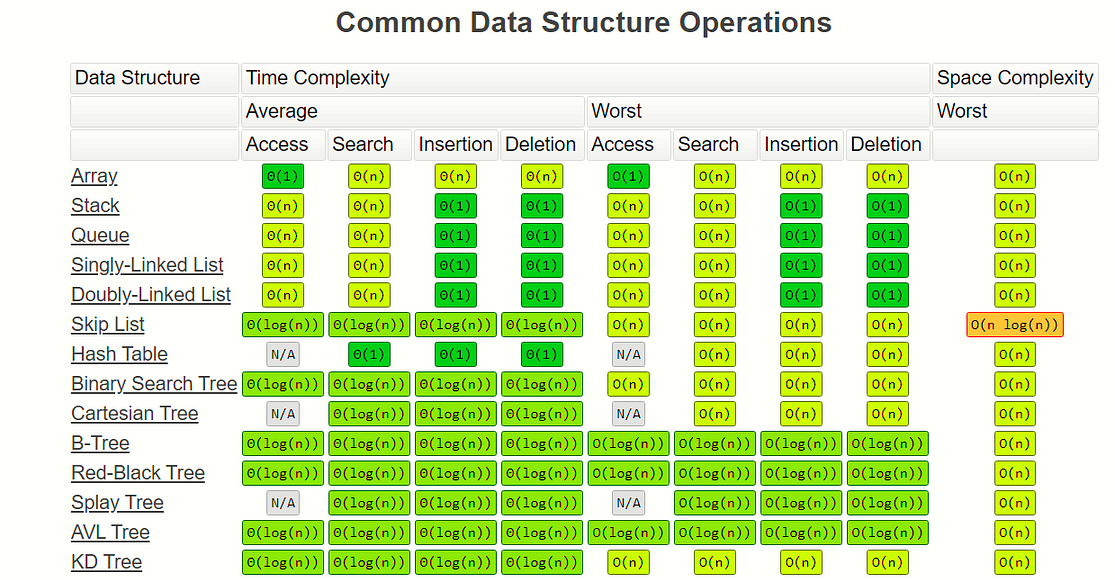
For a more complete guide… checkout :
- way we analyze how efficient algorithms are without getting too mired in details
- can model how much time any function will take given n inputs
- interested in order of magnitude of number of the exact figure
- O absorbs all fluff and n = biggest term
- Big O of 3x^2 +x + 1 = O(n^2)
Time Complexity
no loops or exit & return = O(1)
0 nested loops = O(n) 1 nested loops = O(n^2) 2 nested loops = O(n^3) 3 nested loops = O(n^4)
recursive: as you add more terms, increase in time as you add input diminishes recursion: when you define something in terms of itself, a function that calls itself
- used because of ability to maintain state at diffferent levels of recursion
- inherently carries large footprint
- every time function called, you add call to stack
iterative: use loops instead of recursion (preferred) - favor readability over performance
O(n log(n)) & O(log(n)): dividing/halving
- if code employs recursion/divide-and-conquer strategy
- what power do i need to power my base to get n
Time Definitions
- constant: does not scale with input, will take same amount of time
- for any input size n, constant time performs same number of operations every time
- logarithmic: increases number of operations it performs as logarithmic function of input size n
- function log n grows very slowly, so as n gets longer, number of operations the algorithm needs to perform doesn’t increase very much
- halving
- linear: increases number of operations it performs as linear function of input size n
- number of additional operations needed to perform grows in direct proportion to increase in input size n
- log-linear: increases number of operations it performs as log-linear function of input size n
- looking over every element and doing work on each one
- quadratic: increases number of operations it performs as quadratic function of input size n
- exponential: increases number of operations it performs as exponential function of input size n
- number of nested loops increases as function of n
- polynomial: as size of input increases, runtime/space used will grow at a faster rate
- factorial: as size of input increases, runtime/space used will grow astronomically even with relatively small inputs
- rate of growth: how fast a function grows with input size
Space Complexity
- How does the space usage scale/change as input gets very large?
- What auxiliary space does your algorithm use or is it in place (constant)?
- Runtime stack space counts as part of space complexity unless told otherwise.
